Proof that
Start with the identity
Convert both sides of the equation into the vulgar fractions
Apply square roots on both sides to yield
Multiply both sides by  to obtain
to obtain
Any number's square root squared gives the original number, so

- *see the title link for the solution

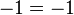

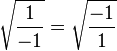
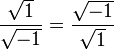


No comments:
Post a Comment